Polar plots using Python and Matplotlib

Overview:

A point in polar co-ordinates is represented as (r,Θ).
The pair has a distance and angle – r for radius or distance from the origin and theta - Θ for the angle at which r has to be measured from origin.
Polar co-ordinates and their modified counterparts are used in navigation, in describing the directionality of a microphone and in any system that is based on a central-point or origin.
The pyplot module of Python Matplotlib provides the function polar which draws a polar plot.
Remember, any mathematical function that can be plotted using the Cartesian coordinate system can be plotted using the polar co-ordinates as well.

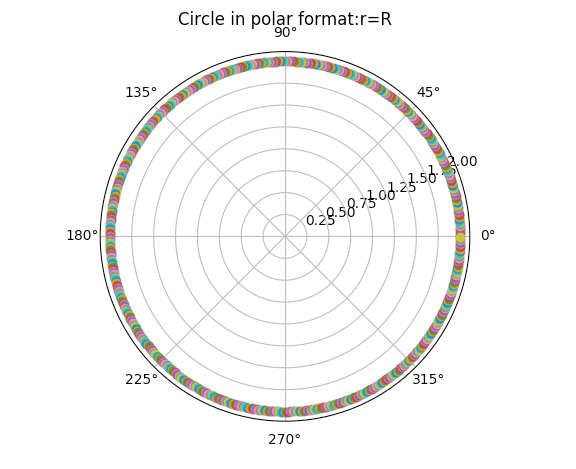
Example1- Circle:

The python code below plots a circle using polar form. The equation of the circle in polar form is given by r = R.

# Example Python Program to plot a polar plot of a circle

# import the numpy and pyplot modules
import numpy as np
import matplotlib.pyplot as plot

plot.axes(projection='polar')

# Set the title of the polar plot
plot.title('Circle in polar format:r=R')

# Plot a circle with radius 2 using polar form
rads = np.arange(0, (2*np.pi), 0.01)

for radian in rads:
plot.polar(radian,2,'o')

# Display the Polar plot
plot.show()

Output1-Circle:

Circle in polar form

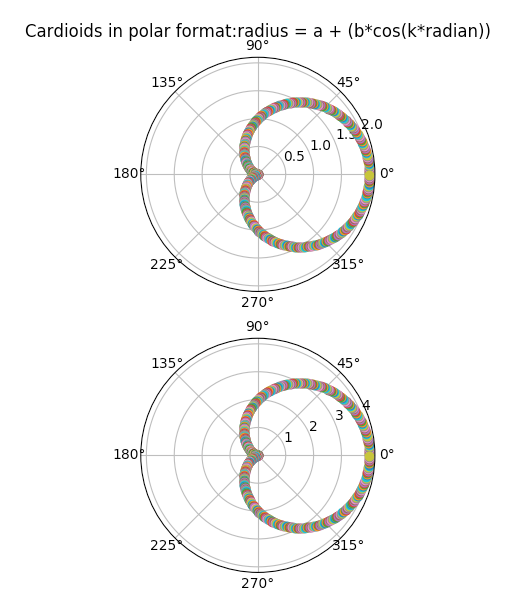
Example2-Cardioids-Symmetrical around x-axis:

When the radii of two circles are equal, and when one circle is fixed and the other circle is rolling on the first one – a point on the rolling circle traced will plot a cardioid.

The polar forms of the cardioids are given by:

r = a + bcos(k*Θ)

r = a + bsin(k*Θ)

For the equation, r = a + bcos(k*Θ),

When a=1, b=1 and k=1, the cardioids are symmetrical around x-axis on the positive side.

When a=-1, b=-1 and k=1, the cardioids are symmetrical around x-axis on the negative side.

# Example Python Program to plot Cardioids

# import the numpy and pyplot modules

import numpy as np

import matplotlib.pyplot as plot

fig = plot.figure()

fig.add_subplot(211, projection='polar')

# Set the title of the polar plot

plot.title('Cardioids in polar format:radius = a + (b*cos(k*radian))')

# Radian values upto 2*pi

rads = np.arange(0, (2*np.pi), 0.01)

a = 1

b = 1

k = 1

# a = 1 and b = 1

for radian in rads:

radius = a + (b*np.cos(k*radian))

# Plot in polar co-ordinates

plot.polar(radian,radius,'o')

a = a+1

b = b+1

fig.add_subplot(212, projection='polar')

# a = 2 and b = 2

for radian in rads:

radius = a + (b*np.cos(k*radian))

# Plot in polar co-ordinates

plot.polar(radian,radius,'o')

# Display the Polar plot

plot.show()

Output2-Cardioids-Symmetrical around x-axis:

Cardioids - polar plots

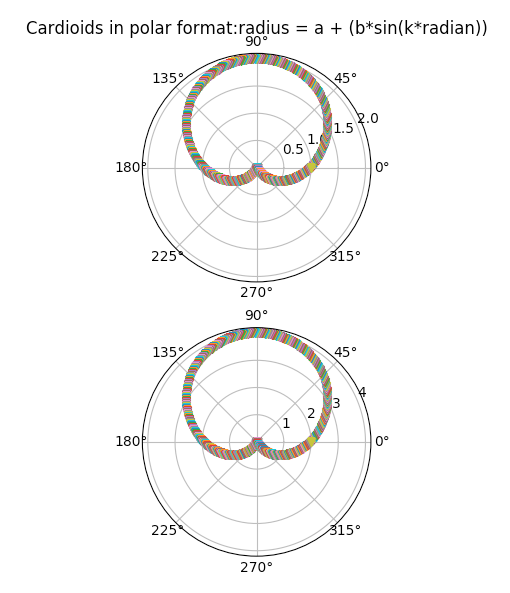
Example3-Cardioids-Symmetrical around y-axis:

# Example Python Program to plot Cardioids that are

# symmetric around y axis

# import the numpy and pyplot modules

import numpy as np

import matplotlib.pyplot as plot

fig = plot.figure()

fig.add_subplot(211, projection='polar')

# Set the title of the polar plot

plot.title('Cardioids in polar format:radius = a + (b*sin(k*radian))')

# Radian values upto 2*pi

rads = np.arange(0, (2*np.pi), 0.01)

a = 1

b = 1

k = 1

# a = -1 and b = -1

for radian in rads:

radius = a + (b*np.sin(k*radian))

# Plot the cardioids in polar co-ordinates

plot.polar(radian, radius, 'v')

a = a+1

b = b+1

fig.add_subplot(212, projection='polar')

# a = -2 and b = -2

for radian in rads:

radius = a + (b*np.sin(k*radian))

# Plot in polar co-ordinates

plot.polar(radian, radius,'v')

# Display the cardioids -

plot.show()

Example3-Cardioids-Symmetrical around y-axis:

Cardioids symmetric around y axis

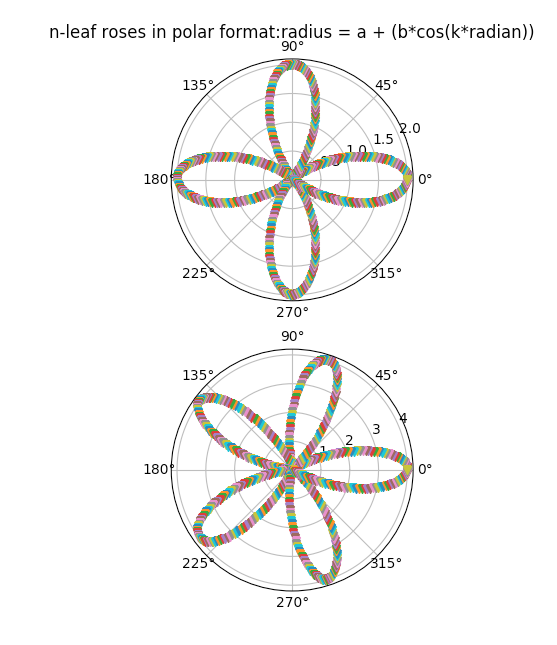
Example4-n-leaf roses:

While keeping k > 1, and a=1,b=1,a=2,b=2 k-leaf roses are plotted.

# Example Python Program to plot Cardioids that are

# symmetric around y axis

# import the numpy and pyplot modules

import numpy as np

import matplotlib.pyplot as plot

fig = plot.figure()

fig.add_subplot(211, projection='polar')

# Set the title of the polar plot

plot.title('k-leaf roses in polar format:radius = a + (b*cos(k*radian))')

# Radian values upto 2*pi

rads = np.arange(0, (2*np.pi), 0.01)

a = 1

b = 1

k = 4

# a = -1 and b = -1

for radian in rads:

radius = a + (b*np.cos(k*radian))

# Plot the cardioids in polar co-ordinates

plot.polar(radian, radius, 'v')

a = a+1

b = b+1

k = 5

fig.add_subplot(212, projection='polar')

# a = -2 and b = -2

for radian in rads:

radius = a + (b*np.cos(k*radian))

# Plot in polar co-ordinates

plot.polar(radian, radius,'v')

# Display the cardioids -

plot.show()

Output5-n-leaf roses:

k-leaf roses